We accept paid Guest & Sponsored Post on our Site : If you want paid guest post or sponsored post on my website, then you can contact us on my email – [email protected]

Decimal to Binary Converter

Use our decimal to binary converter to convert a base 10 number to base 2 along with the steps and formulas used in the conversion.
Free Online tool to Convert Decimal to Binary or vice versa.

  • See More Tools
    • If you use this great tool then please comment and/or like this page.
    Average Rating:     Tool Views: 1876

    Is this tool helpful?
    How can we improve it?

    Subscribe for Latest Tools


    Try Our Other Free Tools

    Guest Posting Sites

    YouTube Tag Extractor

    YT Hashtag Extractor

    YouTube Tag Generator

    YouTube Money Calculator

    YT Trending Worldwide

    YT Trending Videos

    YouTube Title Generator

    PED
    Calculator

    NPV Calculator

    Yield to Maturity Calc

    Boyle's Law Calculator

    Beer Lambert Law Calculator

    Gay-Lussac's Law Calculator

    Tiles Calculator

    CHMOD Calculator

    Article Rewriter

    Tree Age Calculator

    Bowling Strike Rate Calculator

    Salary Increase Calculator

    TVM Calculator

    Text Repeater

    HTML to Markdown

    Hex to IP Address

    BMP to JPG Converter

    Bcrypt Password

    Random MAC Address

    Text to ASCII Converter

    Random Paragraph

    Salary To Hourly Calc

    Hourly To Salary Calc

    Random Sentence

    Decimal to Binary

    Words to Numbers

    Binary to Decimal

    ASCII to Text Converter

    Text to Hex Converter

    Randomize Text Lines

    IP to Hex Converter

    Text Length Calculator

    Random Date Generator

    Batting Strike Rate Calculator

    Required Run Rate Calculator

    Match Net Run Rate Calculator

    DL Method Calculator

    Sleep calculator

    Bowling Average Calc

    Batting Average Calculator

    Run Rate Calculator

    Torque Conversion

    Tiefling Names Generator

    Calories Burned Calc

    Pregnancy Due Date Calculator

    Period calculator

    Conception calculator

    Anniversary Calculator

    Youtube Title Length Checker

    Thumbnail Downloader

    YT Channel ID Finder

    YouTube Downloader

    YouTube Title Extractor

    Youtube Desc Extractor

    Youtube Embed Code Generator

    YouTube Income Calc

    Blog Title Generator

    UTM Builder

    YT Timestamp Link Generator

    AdSense Calculator

    Shoe Size Calculator

    CPC
    Calculator

    Percent Error Calculator

    Percentage Difference Calc

    Percent Off Calculator

    Standard Deviation Calc

    Fraction Calculator

    Hexadecimal Calculator

    Numbers to Letters

    Standard error Calculator

    Tournament Net Run Rate Calc

    Cricket Chirp Converter

    Follow On Calculator

    Economy Rate Calculator

    Day of the Week Calc

    Incorrect Quotes

    100 Days Old Calculator

    24 hour to 12 hour converter

    Leap Year Calculator

    Dog Age Calculator

    Slogan Maker

    Cricket Score Counter

    Random Dice Roller

    Random Color Generator

    ANOVA Calculator

    Slug
    Generator

    Data Unit Converter

    KB to MB Converter

    BMR
    Calculator

    Hosting Bandwidth Calc

    Website Bandwidth Calc

    Download Time Calc

    BBCode Generator

    Comma Separator

    Credit Card Generator

    Search by IFSC Code

    Copy
    Arrow

    Hashtag Counter

    Death calculator

    IQ Calculator

    Random Country

    Keyboard Tester

    Spacebar Counter

    Signature
    Generator

    SLA Uptime Calc

    Percentage Increase Calc

    SVG to Data URI

    Flip
    a Coin

    Meta Length Checker

    Mileage Calculator

    Angle Measurement

    Acceleration Calculator

    Slope Calculator

    Displacement Calculator

    Microwave Cooking Time

    Random Email Generator

    Random Team Generator

    Link
    Extractor

    FAQ Schema Generator

    iFrame
    Generator

    Email
    Extractor

    SSN Extractor

    URL
    Extractor

    Regex Matches Extractor

    Remove
    Empty Lines

    Remove Line Breaks

    Sort
    List

    Random Word Generator

    Username
    Generator

    Random VIN Generator

    Random NBA Player

    Cursive
    Text Generator

    Old English
    Font Generator

    Add Commas to Numbers

    Random String Generator

    Add Line Breaks

    Random Number

    Random port generator

    HTML Escape Unescape

    Remove
    Unwanted

    Remove Punctuation

    Remove Line Breaks

    Remove/Replace Double Quotes

    Remove Characters

    Remove Commas

    Replace lines with commas

    Normalize Unicode Text

    Center
    Text

    Compare Two Lists

    Justify
    Text

    Remove Letter Accents

    Pronounceable
    Password

    Kinetic Energy Calculator

    Lead Time Calculator

    Wind Chill Calculator

    Circle Calculator

    Difference
    Checker

    Find and Replace

    Invisible Character

    Remove Duplicate Lines

    Fancy Text Generator

    Fake Tweet Generator

    Fake Address Generator

    API Key Generator

    CSS Pattern Generator

    RSA Key Generator

    Concatenate
    Text

    Word
    Wrap

    Bold Text Generator

    Dummy Image Generator

    Julian Date Converter

    Italic Text Generator

    Placeholder
    Image

    SHA256 Hash Generator

    Html Tag Remover

    GST
    Calculator

    Numbering
    lines

    Text Reverser

    Exchange Rate Calculator

    Google Ads Revenue Calc

    Lorem Ipsum Generator

    Multiplication Table Generator

    Random IMEI Generator

    Movie Title Generator

    Random Image Generator

    Random
    Aesthetic

    Home Loan
    Calculator

    SWP Calculator

    Future Value Calculator

    Compound Interest Calc

    Mutual Fund Returns Calc

    EBITDA Calculator

    ELSS Calculator

    Simple Interest Calculator

    Dividend Yield Calculator

    HRA Calculator

    ROI Calculator

    TDS Calculator

    PPF Calculator

    EPF Calculator

    NPS Calculator

    SIP Calculator

    Gratuity Calculator

    IRR Calculator

    APY Calculator

    EMI Calculator

    RD Calculator

    FD Calculator

    Lumpsum Calculator

    Flat vs Reducing Rate

    Inflation Calculator

    Car Loan EMI Calculator

    CAPM Calculator

    Love
    Calculator

    Calorie Calculator

    Love
    Meter

    Flames Calculator

    Lucky Number Calculator

    ERA
    Calculator

    Depreciation Calculator

    CAGR Calculator

    Cubic Feet Calculator

    Right Angle Triangle Calc

    Discount Calculator

    Max Heart Rate Calculator

    Half Birthday Calculator

    Body Shape Calculator

    BPM
    Counter

    Unicode
    Converter

    Domain Age Checker

    HTML Encoder Decoder

    Add Prefix & Suffix

    Circle Text Generator

    JSON To CSV

    JSON
    Beautifier

    JSON
    Formatter

    XML
    Formatter

    SQL
    Formatter

    Files URL's Extractor

    HTML
    Formatter

    JSON
    Validator

    JSON
    Prettify

    JSON
    Minifier

    CSS
    Minifier

    CSS
    Beautifier

    JavaScript
    Beautifier

    JavaScript
    Minifier

    CSV To JSON

    Speech time calculator

    Words to Time

    KrutiDev To Unicode

    Krutidev to Chanakya

    Chanakya to KrutiDev

    KrutiDev To Mangal

    Mangal To KrutiDev

    Preeti To Unicode

    Unicode to Preeti

    Unicode To KrutiDev

    CSVJSON To JSON

    Numbers
    Extractor

    Phone Number Extractor

    JSON to PHP

    JSON to JAVA

    JSON to XML

    JSON to YAML

    YAML to JSON

    CSV to XML

    JSON to Protobuf

    Grade
    Calculator

    Text to Hashtags

    Text to Morse Code

    CSV to SQL

    CSV to YAML

    XML to JSON

    Twitter Intent Generator

    Mailto link Generator

    Tombstone
    Generator

    Random Maze Generator

    XML to YAML

    JSON to C#

    SQL To JSON

    SQL To JavaScript

    SQL to MongoDB

    INI to JSON

    INI to XML

    INI to YAML

    Image to Data URI

    Data URI to Image

    Website Page Snooper

    Instagram Bio Generator

    Qr Code Generator

    Reverse Image Search

    Word Counter

    Remove
    Spaces

    Remove All Whitespace

    JPG to PDF

    Convert
    CASE

    Line
    Counter

    Upside Down Text Converter

    HTML Image SRC Generator

    Mime Type Checker

    Multiple URL Opener

    PNG to JPG

    Base64 to PNG Converter

    Base64 to PDF Converter

    Base64 to Image

    JFIF to PNG Converter

    Trillion To Billion Calc

    Trillion To Million Calc

    Trillion To Thousand Calc

    Billion, Million, Trillion Calc

    WEBP to JPG

    WEBP to GIF

    WEBP to PNG

    PNG to BMP

    JPG to WEBP

    PNG to WEBP

    GIF to WEBP

    JPG to PNG

    JPEG to 100KB

    MB to KB converter

    JPEG to 1KB

    JPEG to 5KB

    JPEG to 10KB

    JPEG to 15KB

    JPEG to 20KB

    JPEG to 25KB

    JPEG to 30KB

    JPEG to 35KB

    JPEG to 40KB

    JPEG to 45KB

    JPEG to 50KB

    JPEG to 55KB

    JPEG to 60KB

    JPEG to 65KB

    JPEG to 70KB

    JPEG to 75KB

    JPEG to 80KB

    JPEG to 85KB

    JPEG to 90KB

    JPEG to 95KB

    JPEG to 110KB

    JPEG to 120KB

    JPEG to 130KB

    JPEG to 140KB

    JPEG to 150KB

    JPEG to 160KB

    JPEG to 170KB

    JPEG to 180KB

    JPEG to 190KB

    JPEG to 200KB

    JPEG to 250KB

    JPEG to 300KB

    JPEG to 350KB

    JPEG to 400KB

    JPEG to 450KB

    JPEG to 500KB

    JPEG to 600KB

    JPEG to 700KB

    JPEG to 800KB

    Duplex Box

    Privacy Pages Creator

    Screen
    Resolution

    What is my Browser

    WhatsApp Link Generator

    What's My Browser Size

    Random Quote Generator

    Random
    Address

    What Is My IP Address

    Robots.txt
    Generator

    Meta Tag Generator

    Meta Tags Analyzer

    Keyword
    Suggestion

    HTML Hyperlink Generator

    Link to HTML Hyperink List

    HTML List Generator

    RGB to HEX Converter

    Gradient Background

    HEX to Pantone Converter

    Color Code Picker

    base64
    Utility

    Password Generator

    URL
    Splitter

    3 Ply

    5 Ply

    7 Ply

    PayPal Fee Calculator

    Cutoff Calculator

    FOIR Calculator

    Stripe Fee Calculator

    Percentage
    Calculator

    GCD and LCM Calc

    Proportion
    Calculator

    Age
    Calculator

    Biological Age Calculator

    Unix Timestamp

    XOR Calculator

    Money Counter

    Blood Alcohol Content Calc

    Date Difference Calculator

    Tire Age Calculator

    Mortgage
    Calculator

    Bit
    Calculator

    BOND Calculator

    Profit Margin Calculator

    301 Redirect Code Generator

    Social Share Link Generator

    BMI
    Calculator

    Pregnancy Calculator

    MD5 Hash Generator

    Random MD5 Hashes

    NTLM Hash Generator

    Hashing Calculator

    PGVCL
    Calculator

    Electricity Bill Calculator

    Binary
    Translator

    Tip Calculator

    Convolution calculator

    Probability Calculator

    Arccos Calculator

    Roman Numeral

    Alien
    Translator

    Alien
    text generator

    Angle
    Converter

    Area
    Converter

    Astronomical
    Converter

    Bytes/Bits
    Converter

    Density
    Converter

    Electric Current Converter

    Energy
    Converter

    Hours to Seconds

    Seconds to Hours

    Force
    Converter

    Frequency Wavelength

    Frequency
    Converter

    Fuel
    Converter

    LBS to KG Converter

    KG to LBS Converter

    Length
    Converter

    Mass
    Converter

    Power
    Converter

    Power Set Calculator

    Pressure Converter

    Speed
    Converter

    Temperature
    Converter

    Time
    Converter

    Volume
    Converter

    Weight
    Converter

    Random Bitcoin Address

    Random IP Address

    Random IPv6 Generator

    Random Flag Generator

    Random fraction

    Random Hex generator

    Random Time Generator

    Random UUID Generator

    Random Name Picker

    Numbers to Words

    Random Conversation

    Random Topic Generator

    Boy Name Generator

    How to use this Decimal to Binary Converter Tool?

    How to use Yttags's Decimal to Binary Converter?

    • Step 1: Select the Tool
    Decimal to Binary Converter Step 1
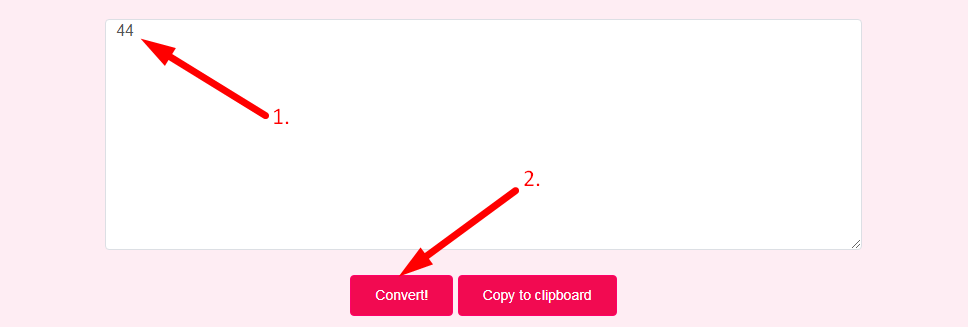
    • Step 2: Enter Decimal Number And Click On Convert Button
    Decimal to Binary Converter Step 2
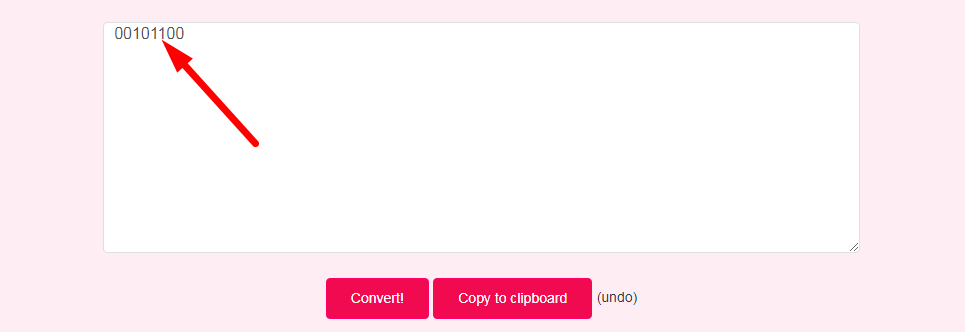
    • Step 3: Check Your Decimal to Binary Converter Result
    Decimal to Binary Converter Step 3

    Decimal to binary conversion table

    here Decimal to Binary Conversion Chart Table

    DecimalBinary
    100000001
    200000010
    300000011
    400000100
    500000101
    600000110
    700000111
    800001000
    900001001
    1000001010
    1100001011
    1200001100
    1300001101
    1400001110
    1500001111
    1600010000
    1700010001
    1800010010
    1900010011
    2000010100
    2100010101
    2200010110
    2300010111
    2400011000
    2500011001
    2600011010
    2700011011
    2800011100
    2900011101
    3000011110
    3100011111
    3200100000
    3300100001
    3400100010
    3500100011
    3600100100
    3700100101
    3800100110
    3900100111
    4000101000
    4100101001
    4200101010
    4300101011
    4400101100
    4500101101
    4600101110
    4700101111
    4800110000
    4900110001
    5000110010
    5100110011
    5200110100
    5300110101
    5400110110
    5500110111
    5600111000
    5700111001
    5800111010
    5900111011
    6000111100
    6100111101
    6200111110
    6300111111
    6401000000
    DecimalBinary
    6501000001
    6601000010
    6701000011
    6801000100
    6901000101
    7001000110
    7101000111
    7201001000
    7301001001
    7401001010
    7501001011
    7601001100
    7701001101
    7801001110
    7901001111
    8001010000
    8101010001
    8201010010
    8301010011
    8401010100
    8501010101
    8601010110
    8701010111
    8801011000
    8901011001
    9001011010
    9101011011
    9201011100
    9301011101
    9401011110
    9501011111
    9601100000
    9701100001
    9801100010
    9901100011
    10001100100
    10101100101
    10201100110
    10301100111
    10401101000
    10501101001
    10601101010
    10701101011
    10801101100
    10901101101
    11001101110
    11101101111
    11201110000
    11301110001
    11401110010
    11501110011
    11601110100
    11701110101
    11801110110
    11901110111
    12001111000
    12101111001
    12201111010
    12301111011
    12401111100
    12501111101
    12601111110
    12701111111
    12810000000
    DecimalBinary
    12910000001
    13010000010
    13110000011
    13210000100
    13310000101
    13410000110
    13510000111
    13610001000
    13710001001
    13810001010
    13910001011
    14010001100
    14110001101
    14210001110
    14310001111
    14410010000
    14510010001
    14610010010
    14710010011
    14810010100
    14910010101
    15010010110
    15110010111
    15210011000
    15310011001
    15410011010
    15510011011
    15610011100
    15710011101
    15810011110
    15910011111
    16010100000
    16110100001
    16210100010
    16310100011
    16410100100
    16510100101
    16610100110
    16710100111
    16810101000
    16910101001
    17010101010
    17110101011
    17210101100
    17310101101
    17410101110
    17510101111
    17610110000
    17710110001
    17810110010
    17910110011
    18010110100
    18110110101
    18210110110
    18310110111
    18410111000
    18510111001
    18610111010
    18710111011
    18810111100
    18910111101
    19010111110
    19110111111
    19211000000
    DecimalBinary
    19311000001
    19411000010
    19511000011
    19611000100
    19711000101
    19811000110
    19911000111
    20011001000
    20111001001
    20211001010
    20311001011
    20411001100
    20511001101
    20611001110
    20711001111
    20811010000
    20911010001
    21011010010
    21111010011
    21211010100
    21311010101
    21411010110
    21511010111
    21611011000
    21711011001
    21811011010
    21911011011
    22011011100
    22111011101
    22211011110
    22311011111
    22411100000
    22511100001
    22611100010
    22711100011
    22811100100
    22911100101
    23011100110
    23111100111
    23211101000
    23311101001
    23411101010
    23511101011
    23611101100
    23711101101
    23811101110
    23911101111
    24011110000
    24111110001
    24211110010
    24311110011
    24411110100
    24511110101
    24611110110
    24711110111
    24811111000
    24911111001
    25011111010
    25111111011
    25211111100
    25311111101
    25411111110
    25511111111

    If you want to link to Decimal To Binary Converter page, please use the codes provided below!

    Decimal To Binary Converter

    FAQs for Decimal to Binary Converter

    What is a Decimal to Binary Converter?
    A Decimal to Binary Converter is a tool that converts decimal (base-10) numbers into binary (base-2) representation, providing a binary equivalent for a given decimal value.
    Why is it important to convert decimals to binary?
    Transferring decimal numbers into binary numbers is important because it can help you and your company communicate with computers effectively. Decimal system numbers refer to those that have a base of 10. These numbers begin at zero and continue to nine.
    What is the rule for converting decimal to binary?
    One of the methods to convert decimal to binary is by dividing the given decimal number recursively by 2. Then, the remainders are noted down till we get 0 as the final quotient. After this step, these remainders are written in reverse order to get the binary value of the given decimal number.
    What is the fastest way to convert binary to decimal?
    Write the binary number and count the power of 2 from right to left, starting from 0 onwards. Now each binary number has the corresponding power of 2 starting from right to left. So the most significant bit will have the highest power of 2. The final answer will be converted into a decimal number that is base 10.
    Why do we convert binary to decimal?
    Because most humans can more readily read and understand decimal being the most common radix used in everyday life, and the computer's natural number system is binary. I assume you keep track of all of your finances in decimal.

    Unit Converters 0

    Converters 0

    Beautifiers 0

    Formatters 0

    Minifiers 0

    Extractors 0

    Finance Calculators 0

    Youtube Tools 0

    Image Tools 0

    SEO Tools 0

    Color Converters 0

    Health Calculators 0

    Text Tools 0

    Website Tools 0

    String Utilities 0

    Number Converters 0

    Generators 0

    Compressors 0

    Others 0

    Calculators 0

    Cricket Calculators0

    Random Tools 0

    Box Calculators 0

    Font Converters 0

    General Tools 0

    Copyright © Yttags.com