Bowling Average Calculator
This free online tool introduces and expounds on the concept of the Bowling Average Calculator in cricket.
To find the number of runs they have conceded per wicket taken.
Number of Runs Conceded
Number of Wickets Taken
If you use this great tool then please comment and/or like this page.
Average Rating: Tool Views: 469
Average Rating: Tool Views: 469
Subscribe for Latest Tools
How to use this Bowling Average Calculator Tool?
How to use Yttags's Bowling Average Calculator?
- Step 1: Select the Tool

- Step 2: Enter The Following Options And Click On Calculate Button.
- Step 3: Check Your Bowling Average Calculator Result
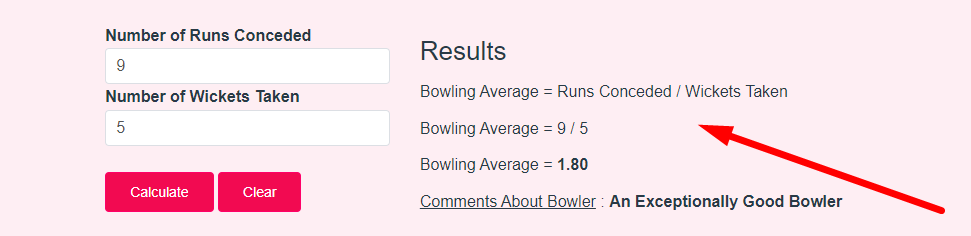
If you want to link to Bowling Average Calculator page, please use the codes provided below!

FAQs for Bowling Average Calculator
What is a Bowling Average Calculator?
A bowling average calculator is a tool used in cricket to determine a bowler's performance by calculating the average number of runs conceded per wicket taken, providing insights into their effectiveness in the game.
How do you calculate average in bowling?
To calculate a bowling average in cricket, divide the total runs conceded by the number of wickets taken, providing an average number of runs conceded per wicket.
How many games does it take to establish a bowling average?
A bowling average in cricket is typically established over several matches, and it becomes more meaningful as a bowler accumulates a larger sample of wickets and runs conceded.
How do they calculate average in cricket?
In cricket, a player's batting average is calculated by dividing the total number of runs scored by the number of times they have been dismissed (outs). A bowler's bowling average is determined by dividing the total runs conceded by the number of wickets they have taken.
What is the law of averages in cricket?
The "law of averages" in cricket is a statistical observation suggesting that players who have performed exceptionally well or poorly in recent games are likely to return to a more typical level of performance in the future, as statistics tend to regress to the mean over time.