Binary to Decimal Converter

Binary to decimal converter tool to convert a binary number to decimal number or vice versa.

  • See More Tools
    • If you use this great tool then please comment and/or like this page.
    Average Rating:     Tool Views: 111

    Is this tool helpful?
    How can we improve it?

    Subscribe for Latest Tools


    How to use this Binary to Decimal Converter Tool?

    How to use Yttags's Binary to Decimal Converter?

    • Step 1: Select the Tool
    Binary to Decimal Converter Step 1
    • Step 2: Enter Binary Number And Click On Convert Button
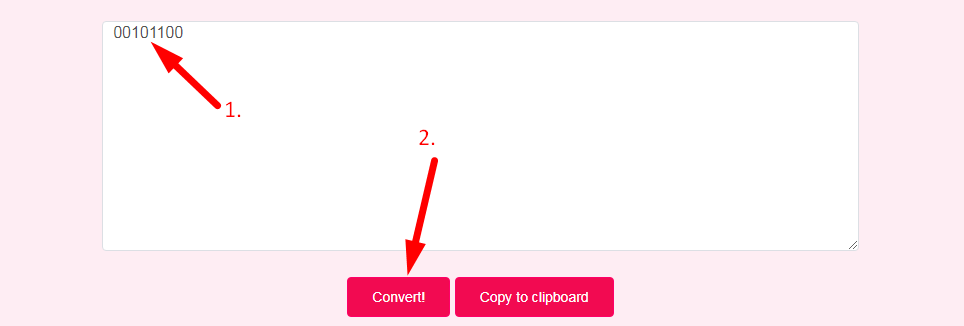
    Binary to Decimal Converter Step 2
    • Step 3: Check Your Binary to Decimal Converter Result
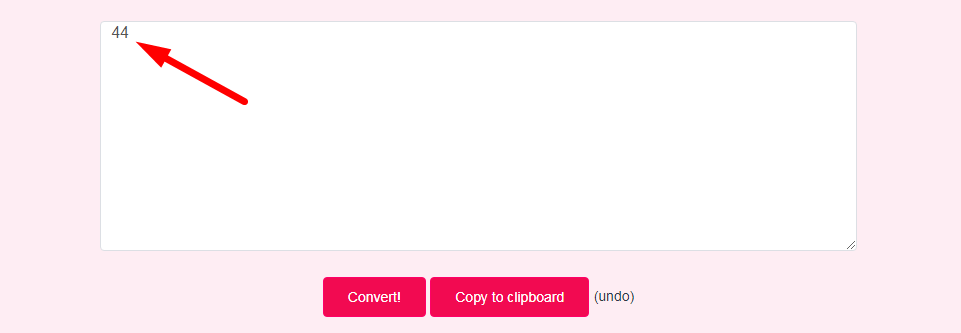
    Binary to Decimal Converter Step 3

    Binary ⇄ decimal converter, step by step conversion, solved examples and methods to learn, practice and verify binary to decimal and decimal to binary conversions.

    Binary Decimal Conversion Chart Table

    BinaryDecimal
    000000011
    000000102
    000000113
    000001004
    000001015
    000001106
    000001117
    000010008
    000010019
    0000101010
    0000101111
    0000110012
    0000110113
    0000111014
    0000111115
    0001000016
    0001000117
    0001001018
    0001001119
    0001010020
    0001010121
    0001011022
    0001011123
    0001100024
    0001100125
    0001101026
    0001101127
    0001110028
    0001110129
    0001111030
    0001111131
    0010000032
    0010000133
    0010001034
    0010001135
    0010010036
    0010010137
    0010011038
    0010011139
    0010100040
    0010100141
    0010101042
    0010101143
    0010110044
    0010110145
    0010111046
    0010111147
    0011000048
    0011000149
    0011001050
    0011001151
    0011010052
    0011010153
    0011011054
    0011011155
    0011100056
    0011100157
    0011101058
    0011101159
    0011110060
    0011110161
    0011111062
    0011111163
    0100000064
    BinaryDecimal
    0100000165
    0100001066
    0100001167
    0100010068
    0100010169
    0100011070
    0100011171
    0100100072
    0100100173
    0100101074
    0100101175
    0100110076
    0100110177
    0100111078
    0100111179
    0101000080
    0101000181
    0101001082
    0101001183
    0101010084
    0101010185
    0101011086
    0101011187
    0101100088
    0101100189
    0101101090
    0101101191
    0101110092
    0101110193
    0101111094
    0101111195
    0110000096
    0110000197
    0110001098
    0110001199
    01100100100
    01100101101
    01100110102
    01100111103
    01101000104
    01101001105
    01101010106
    01101011107
    01101100108
    01101101109
    01101110110
    01101111111
    01110000112
    01110001113
    01110010114
    01110011115
    01110100116
    01110101117
    01110110118
    01110111119
    01111000120
    01111001121
    01111010122
    01111011123
    01111100124
    01111101125
    01111110126
    01111111127
    10000000128
    BinaryDecimal
    10000001129
    10000010130
    10000011131
    10000100132
    10000101133
    10000110134
    10000111135
    10001000136
    10001001137
    10001010138
    10001011139
    10001100140
    10001101141
    10001110142
    10001111143
    10010000144
    10010001145
    10010010146
    10010011147
    10010100148
    10010101149
    10010110150
    10010111151
    10011000152
    10011001153
    10011010154
    10011011155
    10011100156
    10011101157
    10011110158
    10011111159
    10100000160
    10100001161
    10100010162
    10100011163
    10100100164
    10100101165
    10100110166
    10100111167
    10101000168
    10101001169
    10101010170
    10101011171
    10101100172
    10101101173
    10101110174
    10101111175
    10110000176
    10110001177
    10110010178
    10110011179
    10110100180
    10110101181
    10110110182
    10110111183
    10111000184
    10111001185
    10111010186
    10111011187
    10111100188
    10111101189
    10111110190
    10111111191
    11000000192
    BinaryDecimal
    11000001193
    11000010194
    11000011195
    11000100196
    11000101197
    11000110198
    11000111199
    11001000200
    11001001201
    11001010202
    11001011203
    11001100204
    11001101205
    11001110206
    11001111207
    11010000208
    11010001209
    11010010210
    11010011211
    11010100212
    11010101213
    11010110214
    11010111215
    11011000216
    11011001217
    11011010218
    11011011219
    11011100220
    11011101221
    11011110222
    11011111223
    11100000224
    11100001225
    11100010226
    11100011227
    11100100228
    11100101229
    11100110230
    11100111231
    11101000232
    11101001233
    11101010234
    11101011235
    11101100236
    11101101237
    11101110238
    11101111239
    11110000240
    11110001241
    11110010242
    11110011243
    11110100244
    11110101245
    11110110246
    11110111247
    11111000248
    11111001249
    11111010250
    11111011251
    11111100252
    11111101253
    11111110254
    11111111255

    If you want to link to Binary To Decimal Converter page, please use the codes provided below!

    Binary To Decimal Converter

    FAQs for Binary to Decimal Converter

    What is a Binary to Decimal Converter?
    A Binary to Decimal Converter is a tool that transforms binary (base-2) numbers into their decimal (base-10) equivalents, facilitating the conversion between these two number systems.
    What is the fastest way to convert binary to decimal?
    Write the binary number and count the power of 2 from right to left, starting from 0 onwards. Now each binary number has the corresponding power of 2 starting from right to left. So the most significant bit will have the highest power of 2. The final answer will be converted into a decimal number that is base 10.
    Is it possible to convert binary to decimal?
    To convert a binary number to decimal we need to perform a multiplication operation on each digit of a binary number from right to left with powers of 2 starting from 0 and add each result to get the decimal number of it.
    What is the algorithm for converting binary to decimal?
    The formula to convert a binary number to decimal involves multiplying each binary digit by the corresponding power of 2 and summing up the results. For example, to convert the binary number "1010" to decimal: (1 2^3) + (0 2^2) + (1 2^1) + (0 2^0) = 8 + 0 + 2 + 0 = 10. 3.
    Why is binary faster?
    A binary file is usually very much smaller than a text file that contains an equivalent amount of data. I/O with smaller files is faster, too, since there are fewer bytes to move.