Discover the essential trigonometry table including sine, cosine, tangent, and their reciprocal values. Learn formulas and techniques to easily derive trigonometric ratios for angles from 0 to 360 degrees.
Trigonometry(Trikonmiti) Tables to 360: Rules for Finding Trigonometry Tables – Trigonometry(Trikonmiti) is such a special branch of mathematics, in which the relationship between the length and angles of a triangle is studied. It is usually associated with a right triangle, where one angle is always equal to 90 degrees. Trikonmity Table helps to find the palm of angles.
There are more uses of trigonometric tables in other areas of mathematics as well. Because, using the table of trigonometric formulas and functions, many geometrical calculations can be easily solved.
Actually, trigonometric ratios apply only to right-angled triangles, one of which is equal to 90° and the other is acute. Here all the important values, formulas, ratios etc. related to trigonometry(Trikonmiti) table are described which is necessary for class 10th, 11th and 12th.
What is a trigonometry(trikonmiti) table?
The trigonometric ratio table is a collection of values of trigonometric ratios for various standard angles, including other angles such as 0°, 30°, 45°, 60° and 90°. Which is used to find the value of trigonometric sides and angles.
In general, the values of trigonometric ratios of standard angles are necessary to solve trigonometry problems. Therefore, it is necessary to remember the values of the trigonometric ratios of these standard angles.
It consists of trigonometric ratios sin, cos, tan, cosec, sec and cot which establish a relation with Angle. As; sin 0°, cos 30°, tan 45° etc.
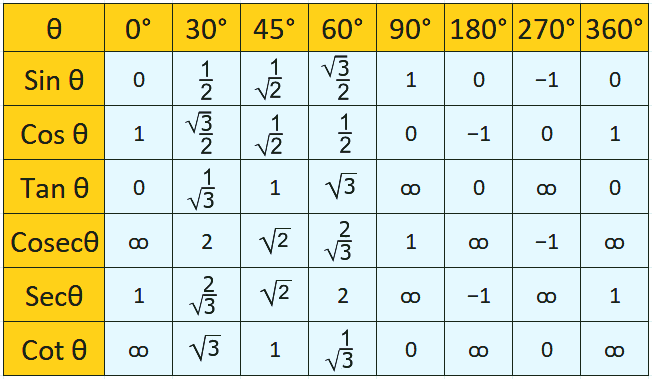
Trigonometry tables up to 360
The easiest way to find the trigonometry table is given below, which you can find by solving it.
| who | 0° | 30° | 45° | 60° | 90° |
| Signal | √(0/4) | √(1/4) | √(2/4) | √(3/4) | √(4/4) |
You can easily extract the value by solving the indicated trigonometry table, as shown below.
| who | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| radian | 0° | p/6 | p/4 | p/3 | p/2 | Pi | 3p/2 | 2 p |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Value up to 360 degree is given above. But using the formula, you can easily calculate the value up to 90 degrees. The values of all the tables will be taken out one by one.
Tricks to remember trigonometry(Trikonmiti) tables
Memorizing the trigonometry OR Trikonmiti table helps in many ways. But the problem is how to remember it. Therefore, it is necessary to remember some formula. which is like this.
- 1/cos x = sec x
- 1/sin x = cosec x
- 1/tan x = cot x
- cos x = sin (90° – x)
- cosec x = sec (90° – x)
- cot x = cos x / sin x
- cot x = tan (90° – x)
- sec x = cosec (90° – x)
- sin x = cos (90° – x)
- tan x = cot (90° – x)
- tan x = sin x / cos
This formula helps in remembering and extracting trigonometric angles.
Step 1. How to find the table of sin
To extract the value of Sin in the Trikonmity Table, keeping 0, 1, 2, 3, 4 on the fraction of √(0/4) has to be divided by 4. As;
| Angles | 0° | 30° | 45° | 60° | 90° |
| solve it | √(0/4) | √(1/4) | √(2/4) | √(3/4) | √(4/4) |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 |
Sin table is easily removed only by solving the middle value.
Step 2. How to find the table of cos
Value of Cos works opposite to Sin. So, starting with √(4/4) instead of starting with √(0/4).
By following this rule all the tables of Cos can be derived.
| Angles | 0° | 30° | 45° | 60° | 90° |
| solve it | √(4/4) | √(3/4) | √(2/4) | √(1/4) | √(0/4) |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 |
Step 3. How to calculate tan table
Tan x = sin x / cos x formula is used to extract the table of tan. This formula is used according to Angle. If 0° is to be extracted, then its value is kept. As;
Tan 0° = sin 0° / cos 0° => put the values of sin 0° and cos 0° here.
That is, sin 0° / cos 0° = 0/1 = > 0
Similarly, the value of all the angles of Tan is calculated. As;
| Angles | 0° | 30° | 45° | 60° | 90° |
| tan | 0 | 1/√3 | 1 | √3 | ∞ |
Step 4. How to find the cot table
The value of Cot is equal to the reciprocal of Tan. If the value of Tan 0° is 0, then the value of Cosec 0° will be 1/0.
From the formula, Cot x = 1/tan x
| Angles | 0° | 30° | 45° | 60° | 90° |
| cot | ∞ | √3 | 1 | 1/√3 | 0 |
Step 5. How to find Cosec Table?
The value of Cosec is equal to the reciprocal of Sin. If the value of Sin 0° is 0, then the value of Cot 0° will be 1/0.
From the formula, Cosec x = 1/sin x
= Cosec 0° = 1/0 => ∞
| Angles | 0° | 30° | 45° | 60° | 90° |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 |
Step 6. How to extract table of sec
The value of Sec is equal to the reciprocal of Cos. If the value of Cos 0° is 1, then the value of Sec 0° will be 1/1.
From the formula, Sec x = 1/cos x
= Sec 0° = 1/1 => 1
| Angles | 0° | 30° | 45° | 60° | 90° |
| sec | 1 | 2/√3 | √2 | 2 | ∞ |
You can also easily calculate the value by using the rules of the given Trikonmiti table. After studying this rule there will be no need to remember Value. So, practice with it and calculate the value of Trikonmiti Table by yourself. If there is any doubt, then do comment us.
Conclusion
In conclusion, understanding the trigonometry table and its associated formulas is crucial for solving various mathematical problems, especially those involving triangles and angles. By memorizing the trigonometric ratios and employing the reciprocal relationships and complementary angle properties, one can efficiently derive the values for angles ranging from 0 to 360 degrees. Regular practice and application of these concepts will enhance proficiency in trigonometry and facilitate the solution of complex mathematical problems.
